Longest Common Subsequence: Interactive Dynamic Programming

Description

The Longest Common Subsequence (LCS) algorithm finds the longest subsequence common to two sequences. Unlike substrings, subsequences are not required to occupy consecutive positions within the original sequences. It's a classic dynamic programming problem with applications in bioinformatics and file comparison.

History

The Longest Common Subsequence problem emerged in the early days of computer science, particularly in the context of computational biology and text comparison. The dynamic programming solution was first formalized in the 1970s. The algorithm gained significant importance with the rise of bioinformatics, where it's used to compare DNA sequences and identify evolutionary relationships. It also became fundamental in the development of diff tools for version control systems. Today, LCS remains a cornerstone algorithm in sequence comparison, file differencing, and various applications in computational biology.

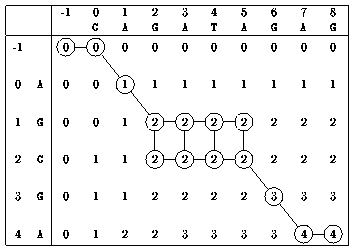
How It Works

Initialize DP Table:
- Create a table of size (m+1) × (n+1)
- Initialize first row and column with zeros
Fill DP Table:
- Compare characters from both sequences
- If characters match, add 1 to diagonal value
- If not, take maximum of left and top cells
Build Solution:
- Start from bottom-right cell
- Trace back to construct the subsequence

Visualization

Speed:

Click Start to begin visualization

Implementation


def lcs(X, Y):
    m, n = len(X), len(Y)
    dp = [[0] * (n + 1) for _ in range(m + 1)]
    
    # Fill dp table
    for i in range(1, m + 1):
        for j in range(1, n + 1):
            if X[i-1] == Y[j-1]:
                dp[i][j] = dp[i-1][j-1] + 1
            else:
                dp[i][j] = max(dp[i-1][j], dp[i][j-1])
    
    # Reconstruct the LCS
    lcs = []
    i, j = m, n
    while i > 0 and j > 0:
        if X[i-1] == Y[j-1]:
            lcs.append(X[i-1])
            i -= 1
            j -= 1
        elif dp[i-1][j] > dp[i][j-1]:
            i -= 1
        else:
            j -= 1
            
    return ''.join(reversed(lcs))

# Example usage
if __name__ == "__main__":
    X = "ABCDGH"
    Y = "AEDFHR"
    print(f"LCS of {X} and {Y} is {lcs(X, Y)}")


#include <string>
#include <vector>
#include <algorithm>
#include <iostream>

std::string lcs(const std::string& X, const std::string& Y) {
    int m = X.length();
    int n = Y.length();
    
    // Create DP table
    std::vector<std::vector<int>> dp(m + 1, std::vector<int>(n + 1, 0));
    
    // Fill dp table
    for(int i = 1; i <= m; i++) {
        for(int j = 1; j <= n; j++) {
            if(X[i-1] == Y[j-1]) {
                dp[i][j] = dp[i-1][j-1] + 1;
            } else {
                dp[i][j] = std::max(dp[i-1][j], dp[i][j-1]);
            }
        }
    }
    
    // Reconstruct the LCS
    std::string lcs;
    int i = m, j = n;
    while(i > 0 && j > 0) {
        if(X[i-1] == Y[j-1]) {
            lcs = X[i-1] + lcs;
            i--; j--;
        } else if(dp[i-1][j] > dp[i][j-1]) {
            i--;
        } else {
            j--;
        }
    }
    
    return lcs;
}

int main() {
    std::string X = "ABCDGH";
    std::string Y = "AEDFHR";
    
    std::cout << "String 1: " << X << std::endl;
    std::cout << "String 2: " << Y << std::endl;
    std::cout << "LCS: " << lcs(X, Y) << std::endl;
    
    return 0;
}


using System;

public class LCS {
    public static string FindLCS(string X, string Y) {
        int m = X.Length;
        int n = Y.Length;
        
        // Create DP table
        int[,] dp = new int[m + 1, n + 1];
        
        // Fill dp table
        for(int i = 1; i <= m; i++) {
            for(int j = 1; j <= n; j++) {
                if(X[i-1] == Y[j-1]) {
                    dp[i,j] = dp[i-1,j-1] + 1;
                } else {
                    dp[i,j] = Math.Max(dp[i-1,j], dp[i,j-1]);
                }
            }
        }
        
        // Reconstruct the LCS
        char[] lcs = new char[dp[m,n]];
        int index = dp[m,n];
        int i = m, j = n;
        
        while(i > 0 && j > 0) {
            if(X[i-1] == Y[j-1]) {
                lcs[--index] = X[i-1];
                i--; j--;
            } else if(dp[i-1,j] > dp[i,j-1]) {
                i--;
            } else {
                j--;
            }
        }
        
        return new string(lcs);
    }
    
    public static void Main(string[] args) {
        string X = "ABCDGH";
        string Y = "AEDFHR";
        
        Console.WriteLine($"String 1: {X}");
        Console.WriteLine($"String 2: {Y}");
        Console.WriteLine($"LCS: {FindLCS(X, Y)}");
    }
}

Applications

DNA sequence alignment in bioinformatics
File difference comparison (diff tools)
Version control systems
Speech recognition
Pattern recognition in time series data

Complexity Analysis

Case	Time Complexity	Description
Best Case	Ω(mn)	Always needs to fill entire DP table
Average Case	Θ(mn)	Requires comparing all character pairs
Worst Case	O(mn)	Same as other cases due to DP approach
Space Complexity	O(mn)	Requires DP table of size m×n

Notes:

m - Length of first sequence
n - Length of second sequence
Space can be optimized to O(min(m,n))
Time complexity is optimal for the general case
Performance is independent of sequence content

Quick Info

Longest Common Subsequence