Radix Sort
Description
Radix Sort is a non-comparative integer sorting algorithm that sorts data by processing each digit position, starting from the least significant digit to the most significant digit. It uses counting sort as a subroutine to sort elements based on their digits at different positions.
History
Radix Sort's origins can be traced back to the early days of mechanical data processing. It was first used with punch card sorting machines in the 1880s by Herman Hollerith. The method was particularly important during the early computer era when sorting large volumes of punch card data was a common task. The algorithm gained prominence in computer science during the 1950s and 1960s with the advent of digital computers. It was particularly useful for sorting fixed-length records with multiple sort keys, such as dates or social security numbers. The term "radix" refers to the base of the number system being used (typically base 10 for decimal numbers or base 2 for binary numbers). The algorithm's efficiency in sorting integers and fixed-length strings has made it a fundamental part of many large-scale sorting applications.
How It Works
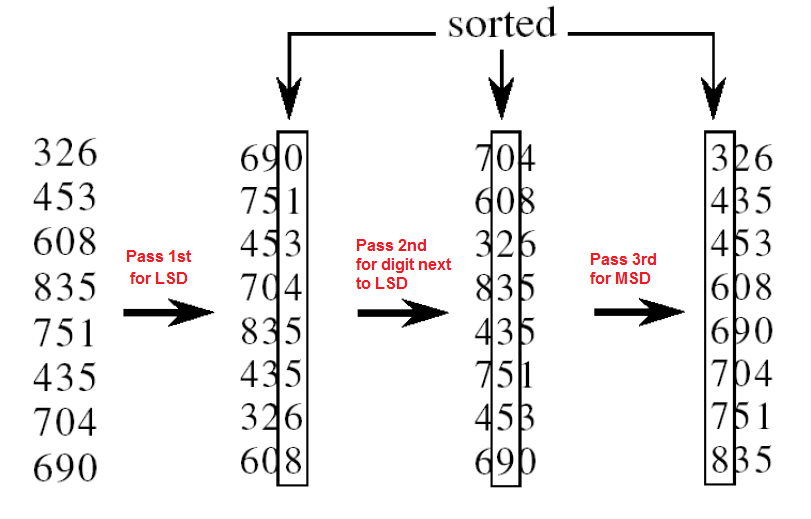
- Digit Processing:
- Start with least significant digit (ones place)
- Move towards most significant digit
- Use counting sort for each digit position
- For Each Digit:
- Create 10 buckets (0-9)
- Distribute numbers to buckets based on current digit
- Collect numbers from buckets in order
- Completion:
- Repeat until all digit positions are processed
- Array will be fully sorted
Visualization
Click Start to begin visualization
Implementation
def counting_sort_by_digit(arr, exp):
n = len(arr)
output = [0] * n
count = [0] * 10
# Store count of occurrences in count[]
for i in range(n):
index = arr[i] // exp
count[index % 10] += 1
# Change count[i] so that count[i] contains actual
# position of this digit in output[]
for i in range(1, 10):
count[i] += count[i - 1]
# Build the output array
i = n - 1
while i >= 0:
index = arr[i] // exp
output[count[index % 10] - 1] = arr[i]
count[index % 10] -= 1
i -= 1
# Copy the output array to arr[]
for i in range(n):
arr[i] = output[i]
def radix_sort(arr):
# Find the maximum number to know number of digits
max_num = max(arr)
# Do counting sort for every digit
exp = 1
while max_num // exp > 0:
counting_sort_by_digit(arr, exp)
exp *= 10
return arr
# Example usage
if __name__ == "__main__":
arr = [170, 45, 75, 90, 802, 24, 2, 66]
print("Original array:", arr)
radix_sort(arr)
print("Sorted array:", arr)
#include <vector>
#include <algorithm>
#include <iostream>
void countingSortByDigit(std::vector<int>& arr, int exp) {
int n = arr.size();
std::vector<int> output(n);
std::vector<int> count(10, 0);
// Store count of occurrences in count[]
for(int i = 0; i < n; i++)
count[(arr[i] / exp) % 10]++;
// Change count[i] so that count[i] contains actual
// position of this digit in output[]
for(int i = 1; i < 10; i++)
count[i] += count[i - 1];
// Build the output array
for(int i = n - 1; i >= 0; i--) {
output[count[(arr[i] / exp) % 10] - 1] = arr[i];
count[(arr[i] / exp) % 10]--;
}
// Copy the output array to arr[]
for(int i = 0; i < n; i++)
arr[i] = output[i];
}
void radixSort(std::vector<int>& arr) {
// Find the maximum number to know number of digits
int max_num = *std::max_element(arr.begin(), arr.end());
// Do counting sort for every digit
for(int exp = 1; max_num/exp > 0; exp *= 10)
countingSortByDigit(arr, exp);
}
int main() {
std::vector<int> arr = {170, 45, 75, 90, 802, 24, 2, 66};
std::cout << "Original array: ";
for(int num : arr) std::cout << num << " ";
radixSort(arr);
std::cout << "\nSorted array: ";
for(int num : arr) std::cout << num << " ";
return 0;
}
public class RadixSort
{
private static void CountingSortByDigit(int[] arr, int exp)
{
int n = arr.Length;
int[] output = new int[n];
int[] count = new int[10];
// Store count of occurrences in count[]
for(int i = 0; i < n; i++)
count[(arr[i] / exp) % 10]++;
// Change count[i] so that count[i] contains actual
// position of this digit in output[]
for(int i = 1; i < 10; i++)
count[i] += count[i - 1];
// Build the output array
for(int i = n - 1; i >= 0; i--)
{
output[count[(arr[i] / exp) % 10] - 1] = arr[i];
count[(arr[i] / exp) % 10]--;
}
// Copy the output array to arr[]
for(int i = 0; i < n; i++)
arr[i] = output[i];
}
public static void Sort(int[] arr)
{
// Find the maximum number to know number of digits
int max_num = arr.Max();
// Do counting sort for every digit
for(int exp = 1; max_num/exp > 0; exp *= 10)
CountingSortByDigit(arr, exp);
}
public static void Main(string[] args)
{
int[] arr = { 170, 45, 75, 90, 802, 24, 2, 66 };
Console.WriteLine("Original array: " + string.Join(" ", arr));
Sort(arr);
Console.WriteLine("Sorted array: " + string.Join(" ", arr));
}
}
Applications
- Sorting integers with fixed number of digits
- Sorting strings of same length
- Processing numerical data in scientific computing
- Sorting dates and timestamps
- Database indexing and sorting
Advantages and Disadvantages
Advantages
- Linear time complexity for fixed-length integers
- Stable sorting algorithm
- Efficient for integers or strings with fixed-length
- Can be faster than comparison sorts
Disadvantages
- Not in-place sorting
- Requires extra space
- Only works with discrete values
- Performance depends on number of digits
Complexity Analysis
| Case | Time Complexity | Description |
|---|---|---|
| Best Case | Ω(d * (n + k)) | When all numbers have same number of digits (d). Here, k is range of each digit (usually 10) |
| Average Case | Θ(d * (n + k)) | Same as best case, as number of operations doesn't depend on input arrangement |
| Worst Case | O(d * (n + k)) | When numbers have maximum possible digits (d) |
| Space Complexity | O(n + k) | Requires temporary arrays for counting and output |
Notes:
- d - Number of digits in the largest number
- n - Number of elements in the array
- k - Range of values for each digit (typically 10 for decimal)
- Time complexity is linear when d is constant
- Performance depends heavily on number of digits in input numbers